Loops and Conditional Logic

Overview

Questions

• How can I do the same operations on many different values?
• How can my programs do different things based on data values?

Objectives

• identify and create loops
• use logical statements to allow for decision-based operations in code

This episode contains two lessons:

1. Repeating Actions with Loops
2. Making Choices with Conditional Logic

Repeating Actions with Loops

---

In the episode about visualizing data, we will see Python code that plots values of interest from our first inflammation dataset (inflammation-01.csv), which revealed some suspicious features.

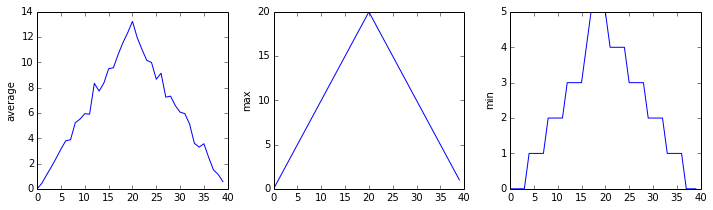
We have a dozen data sets right now and potentially more on the way if Dr. Maverick can keep up their surprisingly fast clinical trial rate. We want to create plots for all of our data sets with a single statement. To do that, we’ll have to teach the computer how to repeat things.

An example task that we might want to repeat is accessing numbers in a list, which we will do by printing each number on a line of its own.

PYTHON

odds = [1, 3, 5, 7]

In Python, a list is basically an ordered collection of elements, and every element has a unique number associated with it — its index. This means that we can access elements in a list using their indices. For example, we can get the first number in the list odds, by using odds[0]. One way to print each number is to use four print statements:

PYTHON

print(odds[0])
print(odds[1])
print(odds[2])
print(odds[3])

OUTPUT

1
3
5
7

This is a bad approach for three reasons:

1. Not scalable. Imagine you need to print a list that has hundreds of elements. It might be easier to type them in manually.

2. Difficult to maintain. If we want to decorate each printed element with an asterisk or any other character, we would have to change four lines of code. While this might not be a problem for small lists, it would definitely be a problem for longer ones.

3. Fragile. If we use it with a list that has more elements than what we initially envisioned, it will only display part of the list’s elements. A shorter list, on the other hand, will cause an error because it will be trying to display elements of the list that do not exist.

PYTHON

odds = [1, 3, 5]
print(odds[0])
print(odds[1])
print(odds[2])
print(odds[3])

PYTHON

1
3
5

ERROR

---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-3-7974b6cdaf14> in <module>()
      3 print(odds[1])
      4 print(odds[2])
----> 5 print(odds[3])

IndexError: list index out of range

Here’s a better approach: a for loop

PYTHON

odds = [1, 3, 5, 7]
for num in odds:
    print(num)

OUTPUT

1
3
5
7

This is shorter — certainly shorter than something that prints every number in a hundred-number list — and more robust as well:

PYTHON

odds = [1, 3, 5, 7, 9, 11]
for num in odds:
    print(num)

OUTPUT

1
3
5
7
9
11

The improved version uses a for loop to repeat an operation — in this case, printing — once for each thing in a sequence. The general form of a loop is:

PYTHON

for variable in collection:
    # do things using variable, such as print

Using the odds example above, the loop might look like this:

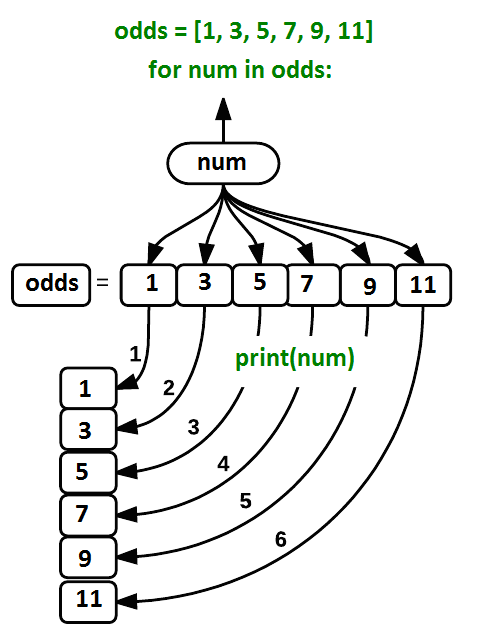
where each number (num) in the variable odds is looped through and printed one number after another. The other numbers in the diagram denote which loop cycle the number was printed in (1 being the first loop cycle, and 6 being the final loop cycle).

We can call the loop variable anything we like, but there must be a colon at the end of the line starting the loop, and we must indent anything we want to run inside the loop. Unlike many other languages, there is no command to signify the end of the loop body (e.g., end for); everything indented after the for statement belongs to the loop.

What’s in a name?

In the example above, the loop variable was given the name num as a mnemonic; it is short for ‘number’. We can choose any name we want for variables. We might just as easily have chosen the name banana for the loop variable, as long as we use the same name when we invoke the variable inside the loop:

PYTHON

odds = [1, 3, 5, 7, 9, 11]
for banana in odds:
   print(banana)

OUTPUT

1
3
5
7
9
11

It is a good idea to choose variable names that are meaningful, otherwise it would be more difficult to understand what the loop is doing.

Here’s another loop that repeatedly updates a variable:

PYTHON

length = 0
names = ['Curie', 'Darwin', 'Turing']
for value in names:
    length = length + 1
print('There are', length, 'names in the list.')

OUTPUT

There are 3 names in the list.

It’s worth tracing the execution of this little program step by step. Since there are three names in names, the statement on line 4 will be executed three times. The first time around, length is zero (the value assigned to it on line 1) and value is Curie. The statement adds 1 to the old value of length, producing 1, and updates length to refer to that new value. The next time around, value is Darwin and length is 1, so length is updated to be 2. After one more update, length is 3; since there is nothing left in names for Python to process, the loop finishes and the print function on line 5 tells us our final answer.

Note that a loop variable is a variable that is being used to record progress in a loop. It still exists after the loop is over, and we can re-use variables previously defined as loop variables as well:

PYTHON

name = 'Rosalind'
for name in ['Curie', 'Darwin', 'Turing']:
    print(name)
print('after the loop, name is', name)

OUTPUT

Curie
Darwin
Turing
after the loop, name is Turing

Note also that finding the length of an object is such a common operation that Python actually has a built-in function to do it called len:

PYTHON

print(len([0, 1, 2, 3]))

OUTPUT

4

len is much faster than any function we could write ourselves, and much easier to read than a two-line loop; it will also give us the length of many other data types we haven’t seen yet, so we should always use it when we can.

From 1 to N

Python has a built-in function called range that generates a sequence of numbers range can accept 1, 2, or 3 parameters.

• If one parameter is given, range generates a sequence of that length, starting at zero and incrementing by 1. For example, range(3) produces the numbers 0, 1, 2.
• If two parameters are given, range starts at the first and ends just before the second, incrementing by one. For example, range(2, 5) produces 2, 3, 4.
• If range is given 3 parameters, it starts at the first one, ends just before the second one, and increments by the third one. For example, range(3, 10, 2) produces 3, 5, 7, 9.

Using range, write a loop that uses range to print the first 3 natural numbers:

OUTPUT

1
2
3

Show me the solution

PYTHON

for number in range(1, 4):
   print(number)

Understanding the loops

Given the following loop:

PYTHON

word = 'oxygen'
for letter in word:
    print(letter)

How many times is the body of the loop executed?

• 3 times
• 4 times
• 5 times
• 6 times

Show me the solution

The body of the loop is executed 6 times.

Computing Powers With Loops

Exponentiation is built into Python:

PYTHON

print(5 ** 3)

OUTPUT

125

Write a loop that calculates the same result as 5 ** 3 using multiplication (and without exponentiation).

Show me the solution

PYTHON

result = 1
for number in range(0, 3):
    result = result * 5
print(result)

Summing a List

Write a loop that calculates the sum of elements in a list by adding each element and printing the final value, so [124, 402, 36] prints 562

Show me the solution

PYTHON

numbers = [124, 402, 36]
summed = 0
for num in numbers:
    summed = summed + num
print(summed)

Computing the Value of a Polynomial

The built-in function enumerate takes a sequence (e.g., a list) and generates a new sequence of the same length. Each element of the new sequence is a pair composed of the index (0, 1, 2,…) and the value from the original sequence:

PYTHON

for idx, val in enumerate(a_list):
    # Do something using idx and val

The code above loops through a_list, assigning the index to idx and the value to val.

Suppose you have encoded a polynomial as a list of coefficients in the following way: the first element is the constant term, the second element is the coefficient of the linear term, the third is the coefficient of the quadratic term, etc.

PYTHON

x = 5
coefs = [2, 4, 3]
y = coefs[0] * x**0 + coefs[1] * x**1 + coefs[2] * x**2
print(y)

OUTPUT

97

Write a loop using enumerate(coefs) which computes the value y of any polynomial, given x and coefs.

Show me the solution

PYTHON

y = 0
for idx, coef in enumerate(coefs):
    y = y + coef * x**idx

Making Choices with Conditional Logic

---

How can we use Python to automatically recognize different situations we encounter with our data and take a different action for each? In this lesson, we’ll learn how to write code that runs only when certain conditions are true.

Conditionals

We can ask Python to take different actions, depending on a condition, with an if statement:

PYTHON

num = 37
if num > 100:
    print('greater')
else:
    print('not greater')
print('done')

OUTPUT

not greater
done

The second line of this code uses the keyword if to tell Python that we want to make a choice. If the test that follows the if statement is true, the body of the if (i.e., the set of lines indented underneath it) is executed, and “greater” is printed. If the test is false, the body of the else is executed instead, and “not greater” is printed. Only one or the other is ever executed before continuing on with program execution to print “done”:

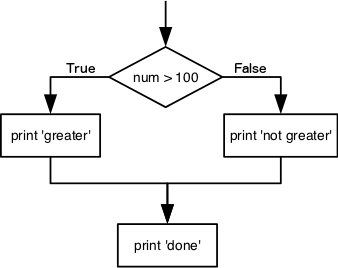
Conditional statements don’t have to include an else. If there isn’t one, Python simply does nothing if the test is false:

PYTHON

num = 53
print('before conditional...')
if num > 100:
    print(num, 'is greater than 100')
print('...after conditional')

OUTPUT

before conditional...
...after conditional

We can also chain several tests together using elif, which is short for “else if”. The following Python code uses elif to print the sign of a number.

PYTHON

num = -3

if num > 0:
    print(num, 'is positive')
elif num == 0:
    print(num, 'is zero')
else:
    print(num, 'is negative')

OUTPUT

-3 is negative

Note that to test for equality we use a double equals sign == rather than a single equals sign = which is used to assign values.

Comparing in Python

Along with the > and == operators we have already used for comparing values in our conditionals, there are a few more options to know about:

• >: greater than
• <: less than
• ==: equal to
• !=: does not equal
• >=: greater than or equal to
• <=: less than or equal to

We can also combine tests using and and or. and is only true if both parts are true:

PYTHON

if (1 > 0) and (-1 >= 0):
    print('both parts are true')
else:
    print('at least one part is false')

OUTPUT

at least one part is false

while or is true if at least one part is true:

PYTHON

if (1 < 0) or (1 >= 0):
    print('at least one test is true')

OUTPUT

at least one test is true

True and False

True and False are special words in Python called booleans, which represent truth values. A statement such as 1 < 0 returns the value False, while -1 < 0 returns the value True.

Checking Our Data

Now that we’ve seen how conditionals work, we can use them to check for the suspicious features we saw in our inflammation data. We are about to use functions provided by the numpy module again. Therefore, if you’re working in a new Python session, make sure to load the module with:

PYTHON

import numpy

From the first couple of plots, we saw that maximum daily inflammation exhibits a strange behavior and raises one unit a day. Wouldn’t it be a good idea to detect such behavior and report it as suspicious? Let’s do that! However, instead of checking every single day of the study, let’s merely check if maximum inflammation in the beginning (day 0) and in the middle (day 20) of the study are equal to the corresponding day numbers.

PYTHON

max_inflammation_0 = numpy.amax(data, axis=0)[0]
max_inflammation_20 = numpy.amax(data, axis=0)[20]

if max_inflammation_0 == 0 and max_inflammation_20 == 20:
    print('Suspicious looking maxima!')

We also saw a different problem in the third dataset; the minima per day were all zero (looks like a healthy person snuck into our study). We can also check for this with an elif condition:

PYTHON

elif numpy.sum(numpy.amin(data, axis=0)) == 0:
    print('Minima add up to zero!')

And if neither of these conditions are true, we can use else to give the all-clear:

PYTHON

else:
    print('Seems OK!')

Let’s test that out:

PYTHON

data = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',')

max_inflammation_0 = numpy.amax(data, axis=0)[0]
max_inflammation_20 = numpy.amax(data, axis=0)[20]

if max_inflammation_0 == 0 and max_inflammation_20 == 20:
    print('Suspicious looking maxima!')
elif numpy.sum(numpy.amin(data, axis=0)) == 0:
    print('Minima add up to zero!')
else:
    print('Seems OK!')

OUTPUT

Suspicious looking maxima!

PYTHON

data = numpy.loadtxt(fname='inflammation-03.csv', delimiter=',')

max_inflammation_0 = numpy.amax(data, axis=0)[0]
max_inflammation_20 = numpy.amax(data, axis=0)[20]

if max_inflammation_0 == 0 and max_inflammation_20 == 20:
    print('Suspicious looking maxima!')
elif numpy.sum(numpy.amin(data, axis=0)) == 0:
    print('Minima add up to zero!')
else:
    print('Seems OK!')

OUTPUT

Minima add up to zero!

In this way, we have asked Python to do something different depending on the condition of our data. Here we printed messages in all cases, but we could also imagine not using the else catch-all so that messages are only printed when something is wrong, freeing us from having to manually examine every plot for features we’ve seen before.

How Many Paths?

Consider this code:

PYTHON

if 4 > 5:
    print('A')
elif 4 == 5:
    print('B')
elif 4 < 5:
    print('C')

Which of the following would be printed if you were to run this code? Why did you pick this answer?

1. A
2. B
3. C
4. B and C

Show me the solution

C gets printed because the first two conditions, 4 > 5 and 4 == 5, are not true, but 4 < 5 is true. In this case, only one of these conditions can be true for at a time, but in other scenarios multiple elif conditions could be met. In these scenarios, only the action associated with the first true elif condition will occur, starting from the top of the conditional section.

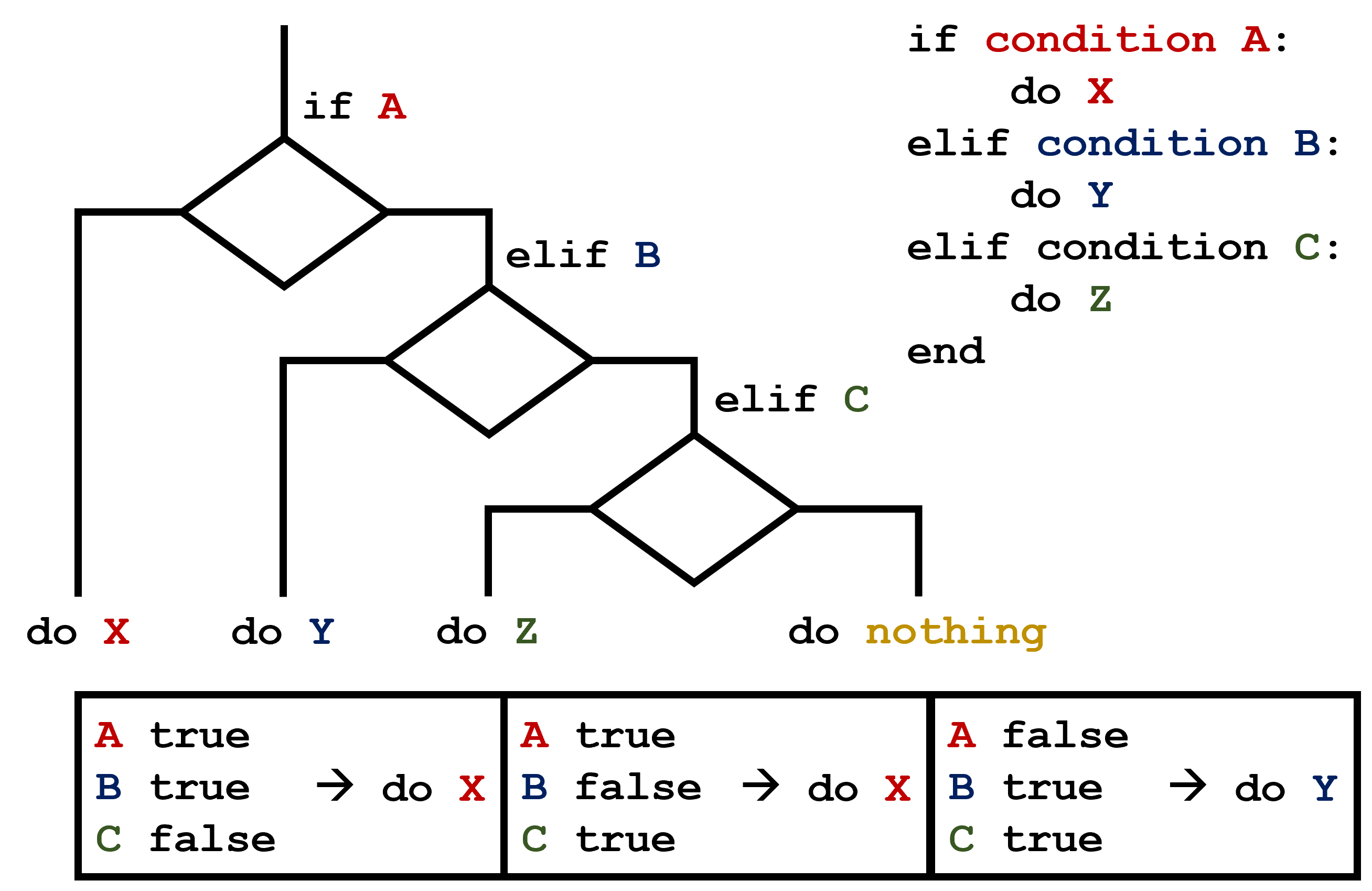
This contrasts with the case of multiple if statements, where every action can occur as long as their condition is met.

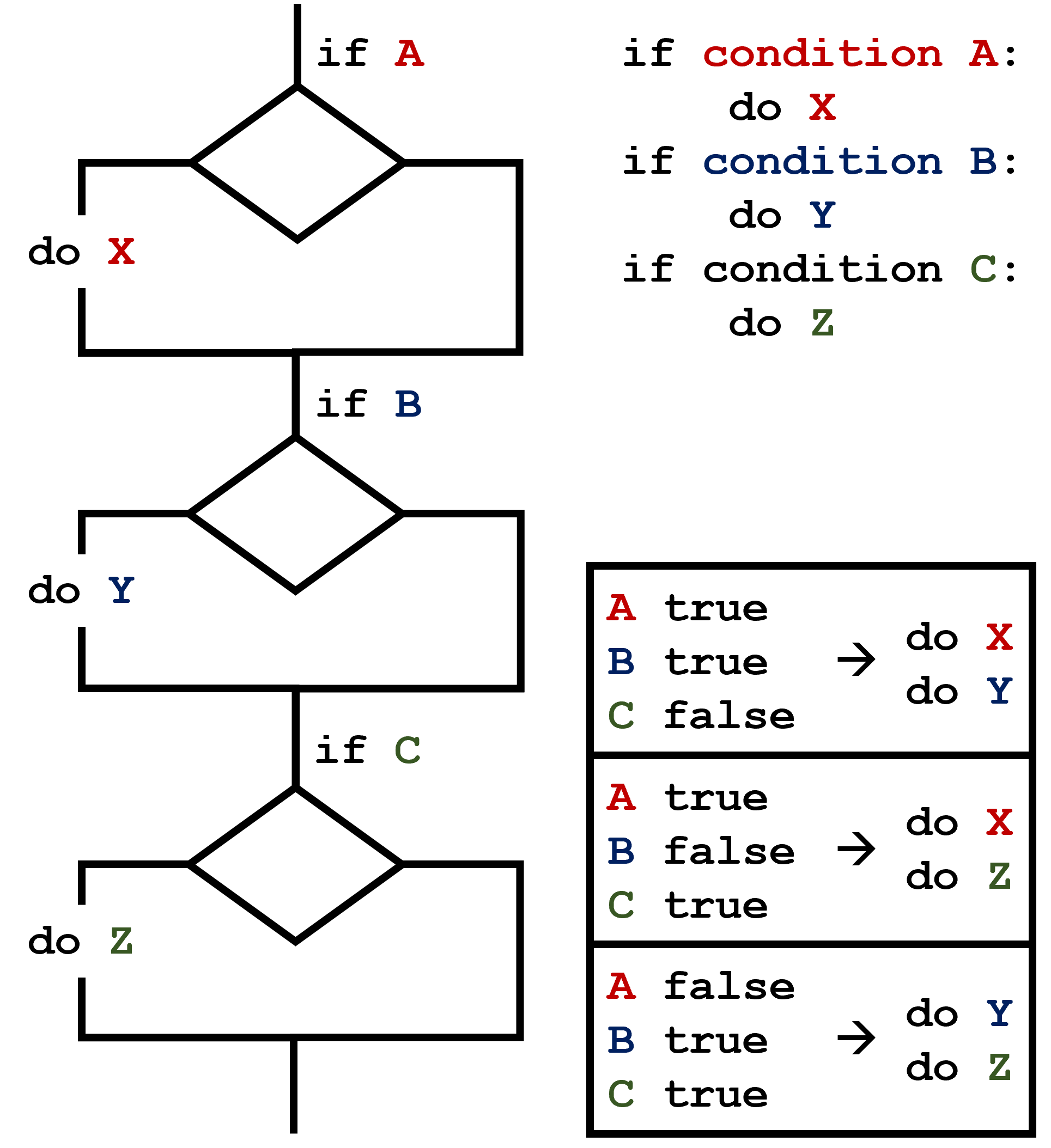
What Is Truth?

True and False booleans are not the only values in Python that are true and false. In fact, any value can be used in an if or elif. After reading and running the code below, explain what the rule is for which values are considered true and which are > considered false.

PYTHON

if '':
    print('empty string is true')
if 'word':
    print('word is true')
if []:
    print('empty list is true')
if [1, 2, 3]:
    print('non-empty list is true')
if 0:
    print('zero is true')
if 1:
    print('one is true')

That’s Not Not What I Meant

Sometimes it is useful to check whether some condition is not true. The Boolean operator not can do this explicitly. After reading and running the code below, write some if statements that use not to test the rule that you formulated in the previous challenge.

PYTHON

if not '':
    print('empty string is not true')
if not 'word':
    print('word is not true')
if not not True:
    print('not not True is true')

Close Enough

Write some conditions that print True if the variable a is within 10% of the variable b and False otherwise. Compare your implementation with your partner’s. Do you get the same answer for all possible pairs of numbers?

Hint

There is a built-in function abs that returns the absolute value of a number:

PYTHON

print(abs(-12))

OUTPUT

12

Solution 1

PYTHON

a = 5
b = 5.1

if abs(a - b) <= 0.1 * abs(b):
    print('True')
else:
    print('False')

Solution 2

PYTHON

print(abs(a - b) <= 0.1 * abs(b))

This works because the Booleans True and False have string representations which can be printed.

In-Place Operators

Python (and most other languages in the C family) provides in-place operators that work like this:

PYTHON

x = 1  # original value
x += 1 # add one to x, assigning result back to x
x *= 3 # multiply x by 3
print(x)

OUTPUT

6

Write some code that sums the positive and negative numbers in a list separately, using in-place operators. Do you think the result is more or less readable than writing the same without in-place operators?

Show me the solution

PYTHON

positive_sum = 0
negative_sum = 0
test_list = [3, 4, 6, 1, -1, -5, 0, 7, -8]
for num in test_list:
    if num > 0:
        positive_sum += num
    elif num == 0:
        pass
    else:
        negative_sum += num
print(positive_sum, negative_sum)

Here pass means “don’t do anything”. In this particular case, it’s not actually needed, since if num == 0 neither sum needs to change, but it illustrates the use of elif and pass.

Sorting a List Into Buckets

In our data folder, large data sets are stored in files whose names start with “inflammation-” and small data sets – in files whose names start with “small-”. We also have some other files that we do not care about at this point. We’d like to break all these files into three lists called large_files, small_files, and other_files, respectively.

Add code to the template below to do this. Note that the string method startswith returns True if and only if the string it is called on starts with the string passed as an argument, that is:

PYTHON

'String'.startswith('Str')

OUTPUT

True

But

PYTHON

'String'.startswith('str')

OUTPUT

False

Use the following Python code as your starting point:

PYTHON

filenames = ['inflammation-01.csv',
         'myscript.py',
         'inflammation-02.csv',
         'small-01.csv',
         'small-02.csv']
large_files = []
small_files = []
other_files = []

Your solution should:

1. loop over the names of the files
2. figure out which group each filename belongs in
3. append the filename to that list

In the end the three lists should be:

PYTHON

large_files = ['inflammation-01.csv', 'inflammation-02.csv']
small_files = ['small-01.csv', 'small-02.csv']
other_files = ['myscript.py']

Show me the solution

PYTHON

for filename in filenames:
    if filename.startswith('inflammation-'):
        large_files.append(filename)
    elif filename.startswith('small-'):
        small_files.append(filename)
    else:
        other_files.append(filename)

print('large_files:', large_files)
print('small_files:', small_files)
print('other_files:', other_files)

Counting Vowels

1. Write a loop that counts the number of vowels in a character string.
2. Test it on a few individual words and full sentences.
3. Once you are done, compare your solution to your neighbor’s. Did you make the same decisions about how to handle the letter ‘y’ (which some people think is a vowel, and some do not)?

Solution

vowels = 'aeiouAEIOU'
sentence = 'Mary had a little lamb.'
count = 0
for char in sentence:
   if char in vowels:
       count += 1

print('The number of vowels in this string is ' + str(count))

{.challenge}

Key Points

• Use for variable in sequence to process the elements of a sequence one at a time.
• The body of a for loop must be indented.
• Use len(thing) to determine the length of something that contains other values.
• Use if condition to start a conditional statement, elif condition to provide additional tests, and else to provide a default.
• The bodies of the branches of conditional statements must be indented.
• Use == to test for equality.
• X and Y is only true if both X and Y are true.
• X or Y is true if either X or Y, or both, are true.
• Zero, the empty string, and the empty list are considered false; all other numbers, strings, and lists are considered true.
• True and False represent truth values.